ASSERVISEMENT 2 AXES
par Florent PAITRAULT
Vous pouvez télécharger le pdf de cette partie ici: Asservisement 2 Axes.pdf
LA DETECTION D'OBSTACLES
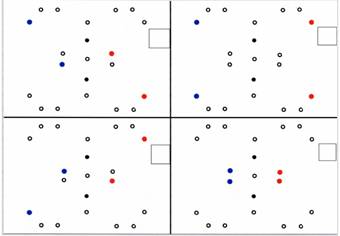
La détection d’obstacle est une partie qui nous a posé beaucoup de problèmes, en effet, nous avons testé pas mal de solutions différentes avant d’en trouver une qui nous convenait.Dans notre cas, le but était de vérifier que le point d’arrivée demandé était bien accessible et si c’est le cas de donner le meilleur chemin a emprunter.En plus des bord du terrain, il fallait éviter 4 totems placés selon l’une des 4 configurations ci-contre (la configuration du match était tirée au sort a chaque nouveau match).
Nous avons remarqué que si notre programme considérait qu’il y avait 8 totems sur le terrain (puisqu’on ne sait jamais quelle configuration est présente), on rendrais inaccessible un trop grand nombre d’endroit.
C’est pourquoi nous avons développé en parallèle un programme de reconnaissance avec la camera qui donnait la configuration dès le départ. Le problème majeur de ceci est que, bien que la reconnaissance marchait très bien à l’ICAM, elle n’a plus très bien fonctionnée à la coupe a cause de la luminosité, des couleurs, des formes qui n’était pas identique à notre table (malgré un réseau de neurone !).
Mon conseil est de réaliser un programme d’évitement qui marche sans reconnaissance préalable, même si il doit être moins performant (la camera n’est pas a l’abri d’une panne).
- Quelques solutions testées :
Voici un petit récapitulatif des solutions testés et rejetés car elles étaient inadaptées pour nous :
- Calcul d’intersection entre le robot et les totems :
C’est un programme assez fastidieux à réaliser qui vérifie si la trajectoire en ligne droite du robot n’est pas coupée par les totems. Cependant, pour simplifier, nous avons considéré la trajectoire comme une droite et pris en compte la largeur du robot dans le diamètre des totems (Dtotem=Dtotem_réél+Diagonale_du_Robot). Cette approximation est bonne si le robot est un cercle mais si c’est un carré, cela réduit les zones où l’on peut aller considérablement.
Si la trajectoire n’est pas bonne il renvoi la position du point de tangence de la trajectoire avec le totem le plus proche.
→ Les problèmes de cette méthode sont qu’elle est complexe ; et qu’elle ne prend pas en compte les bords du terrain et qu’elle conduit a trop de zones impossible dans notre cas (ce programme est en annexes si cela peut vous aider...).
Cette solution, qui peut être trouvée sur Internet, est beaucoup utilisée pour la détection d’obstacle. Cependant, elle repose sur une théorie très lourde et difficilement compréhensible.
Le principe général est de tracer tous les segment entre le point de départ, d’arrivée du robot et les sommets de chaque obstacle (assimilés a des carrés). Ici, cela nous fait 18 point au total et donc 153 segments. Puis, on ne garde que les segments qui ne sont coupé par aucun obstacle. On choisi alors le plus court chemin pour aller du point de départ au point d’arrivé en empruntant ces segments.
→ Les problèmes de cette méthode sont qu’elle est complexe et approxime les obstacles à des carrés (ce programme est en annexes si cela peut vous aider...)..
Ici on affecte des poids aux zones où sont les totems et les bords et l’on modifie la trajectoire du robot selon une fonction qui se sert de ses poids. Par exemple si l’on prend la fonction 1/x, des que l’on s’approche d’une zone avec des totems, la fonction tend vers l’infini et le robot doit alors tourner dans la direction opposé.
→ Les problèmes de cette méthode sont qu’elle doit être implantée directement dans l’asservissement, ce qui risque de le perturber ; qu’on ne peut pas prévoir ce que va faire le robot et qu’elle n’a pas donné de bon résultat à l‘essai.

La solution finale pour laquelle nous avons opté a nécessité un peu de travail mais à l’avantage de rendre les réactions du robot totalement prévisible.
Nous avons découpé le terrain en carrés de la taille du Robot (30cm de coté) et défini pour chaque configuration quelles sont les cases où il est impossible de se rendre (car présence d’un totem).
Nous avons donc obtenu 6×9 cases qui sont centrées sur le plateau, avec une bande de 15 cm de largeur inaccessible tout autour (2×15+9×30 = 300 cm : longueur du plateau et 2×15+6×30 = 210 cm : largeur du plateau).
Puis nous avons tout simplement grisé les cases occupées par les totems pour les 4 configurations. Ainsi, nous avons rempli à la main 4 matrices de 54 lignes par 54 colonnes, une pour chaque configuration, où il y a en ligne les 54 positions de départ possibles et en colonne les 54 positions de d’arrivée possibles.
Le code est le suivant :
- 0 si la trajectoire est directe (pas d’obstacle entre le point de départ et d’arrivé).
- 55 si le point d’arriver est impossible à atteindre (si il se trouve sur un totem).
- Le numéro de la première case où aller pour éviter les obstacles présents sur la trajectoire.
Ces quatre matrices se trouvent dans le fichier Excel nommé « Evitement.xls » si vous en avez besoin.
Le programme qui utilise ces matrices est alors très simple. Selon le point de départ, d’arrivée du robot et la configuration des totems, il lit le nombre correspondant a la bonne case dans une des matrice. Ce nombre lui donne alors la case où il doit amener le robot, et il renvoi donc à l’asservissement la position du centre de la case concernée.
→ Les avantages de cette méthode sont que les actions du robot sont prévisibles, qu’il est facile de modifier ses trajectoires si besoin est, que le programme est très simple et que les approximations faites sont largement acceptables compte tenu de l’utilisation
En conclusion, le programme utilisé pour l’évitement d’obstacle a très bien fonctionné mais le souci majeur est qu’il se basait sur la reconnaissance d’image pour trouver la configuration des totems et que cette dernière à été perturbé une fois à la coupe.
Mis à part cela, les déplacements grâce à cette technique étaient très fluides et très précis.
Annexes
- Programme de calcul d’intersection entre le robot et les totems en C++
#include <cstdlib>
#include <iostream>
#include <math.h>
#include <stdio.h>
#define stop ; system("PAUSE");
using namespace std;
const double cote=(160*sqrt(2)+40); //on utilise comme obstacle un cercle de rayon "cote" (la diagonale du robot réel+totem)
struct Point
{
double X,Y;
double Angle;
};
int main(int argc, char *argv[])
{
bool Erreur=false;
bool Bon=true;
double Dist,DistMin,coteSecu; //les distance sont au carré pour eviter les racines inutiles
int NbTotem=0;
int i=0;
Point position; //position actuelle
Point destination; //position a atteindre
Point destCht; //position a atteindre apres changement de repere
Point centreCht; //position des centres des totems apres changement de repere
Point resultat; //les coords que retourne la fonction
Point Totem[5]; //position des 4 totem + un totem fictif (en dehors de la carte habituellement et dedans si on veux eviter le robot adverse)
bool ListeTotems[5]={0,0,0,0,0}; //liste des totems en colision avec la trajectoire directe
//--------------------------------//
// initialisation des coordonnées //
//--------------------------------//
position.X=0;
position.Y=0;
destination.X=800;
destination.Y=1000;
int ConfigTotem=3 ;
position.Angle=0;
//position des centres des totems
//on adapte l'initialisation en fonction de la configuration des totems detecté
switch (ConfigTotem)
{
case 1:
Totem[0].X=-680;
Totem[0].Y=-1050;
Totem[1].X=100;
Totem[1].Y=-450;
Totem[2].X=-100;
Totem[2].Y=450;
Totem[3].X=680;
Totem[3].Y=1050;
break;
case 2:
Totem[0].X=-680;
Totem[0].Y=-1050;
Totem[1].X=100;
Totem[1].Y=-450;
Totem[2].X=680;
Totem[2].Y=1050;
Totem[3].X=-680;
Totem[3].Y=1050;
break;
case 3:
Totem[0].X=-680;
Totem[0].Y=-1050;
Totem[1].X=680;
Totem[1].Y=1050;
Totem[2].X=100;
Totem[2].Y=450;
Totem[3].X=-680;
Totem[3].Y=1050;
break;
case 4:
Totem[0].X=100;
Totem[0].Y=-450;
Totem[1].X=-100;
Totem[1].Y=-450;
Totem[2].X=100;
Totem[2].Y=450;
Totem[3].X=-100;
Totem[3].Y=450;
break;
}
Totem[4].X=10000;
Totem[4].Y=10000;
//Changement de coordonne pour avoir le centre du robot comme reference (et pas le centre des roues)
position.X=position.X+90*sin(position.Angle);
position.Y=position.Y+90*cos(position.Angle);
//verif que le point de destination n'est pas confondu avec celui de depart (on sait jamais :))
if ((position.X!=destination.X) || (position.Y!=destination.Y))
{
//et qu'il n'est pas en dehors des lmites accessibles
if ((destination.X>(1050-160*sqrt(2))) || (destination.X<-1050+160*sqrt(2)) || (destination.Y>1500-160*sqrt(2)) || (destination.Y<-1500+160*sqrt(2)))
{
Bon=false;
Erreur=true;
resultat.X=position.X;
resultat.Y=position.Y;
}
else
{
printf("-cote: %f-\n\n",cote);
//-------------------------------------------------------//
// Verification de la valididé de la trajectoire directe //
//-------------------------------------------------------//
//changement de repère destination
destCht.X=destination.X-position.X;
destCht.Y=destination.Y-position.Y;
for (i=0;i<5;i++) //pour chaque totem, on verifie si la trajectoire coupe le cercle
{
//changement de repère totem
centreCht.X=Totem[i].X-position.X;
centreCht.Y=Totem[i].Y-position.Y;
//on verifie d'abord si le totem est bien sur le segment de trajectoire et pas avant ou apres
printf("Totem %d:\n",i);
if (((Totem[i].Y+cote)>min(position.Y,destination.Y)) && ((Totem[i].Y-cote)<max(position.Y,destination.Y)))
{
//si la distance entre la trajo et le centre du totem est inferieure a "coté", il y a colision
Dist=(double) (sqrt(((centreCht.X*centreCht.X+centreCht.Y*centreCht.Y)-(((centreCht.X*destCht.X+centreCht.Y*destCht.Y)*(centreCht.X*destCht.X+centreCht.Y*destCht.Y))/(destCht.X*destCht.X+destCht.Y*destCht.Y)))));
if (Dist<cote)
{
Bon=false;
ListeTotems[i]=1; //on retien le totem en colision
}
printf ("Dist: %f; Collision? %d\n",Dist,ListeTotems[i]);
}
}
}
}
//test de validide de la trajo
printf ("\n---> Trajo directe: ");
if (Bon==true)
{
resultat.X=destination.X;
resultat.Y=destination.Y;
printf ("Bonne\n");
}
else
{
printf ("Pas bonne\n");
if (Erreur==0)
{
//---------------------------------------------//
// reperer le totem en colision le plus proche //
//---------------------------------------------//
DistMin=15000;
for (i=0;i<5;i++) //pour chaque totem en colision, on determine la distance et on l'enregistre dans "Dist" si elle est plus petite que les autres
{
if (ListeTotems[i]==1) //si le totem entre en colision
{
Dist=(double) (sqrt((Totem[i].X-position.X)*(Totem[i].X-position.X)+(Totem[i].Y-position.Y)*(Totem[i].Y-position.Y)));
if (Dist<DistMin) //si la distance est plus petite que les autres
{
DistMin=Dist; //on retien la distance
NbTotem=i; //on retien le numero du totem
}
}
}
//--------------------------------------------------//
// Calcul du point de tangence de la trajo au totem //
//--------------------------------------------------//
//changement de repère totem
centreCht.X=Totem[NbTotem].X-position.X;
centreCht.Y=Totem[NbTotem].Y-position.Y;
//on defini le coteSecu afin d'ajouter une marge de securite lors du contournement des totems
coteSecu=cote+30;
//verification que le point de depart n'est pas dans ou a la limite dun totem (impossibilite de tangenter)
if (((position.X-centreCht.X)*(position.X-centreCht.X)+(position.Y-centreCht.Y)*(position.Y-centreCht.Y))<=(coteSecu*coteSecu))
{
Erreur=true;
resultat.X=position.X;
resultat.Y=position.Y;
}
else
{
//premier point de tangence
resultat.Y=(double) (position.Y+((2*centreCht.X*centreCht.X*centreCht.Y+2*centreCht.Y*centreCht.Y*centreCht.Y+2*centreCht.Y*coteSecu*coteSecu+sqrt(4*coteSecu*coteSecu*(3*coteSecu*coteSecu*centreCht.Y*
centreCht.Y+centreCht.X*centreCht.X*centreCht.X*centreCht.X+centreCht.X*centreCht.X*centreCht.Y*centreCht.Y+2*centreCht.X*centreCht.X*coteSecu*coteSecu)))/(2*(centreCht.X*centreCht.X+centreCht.Y*centreCht.Y))));
resultat.X=(double) (position.X+((centreCht.X*centreCht.X+centreCht.Y*centreCht.Y-coteSecu*coteSecu-centreCht.Y*resultat.Y)/centreCht.X));
//verfication que le point est dans les limites accessibles
if ((resultat.X>(1050-160*sqrt(2))) || (resultat.X<-1050+160*sqrt(2)) || (resultat.Y>1500-160*sqrt(2)) || (resultat.Y<-1500+160*sqrt(2)))
{
//deuxieme point de tangence
resultat.Y=(double) (position.Y+((2*centreCht.X*centreCht.X*centreCht.Y+2*centreCht.Y*centreCht.Y*centreCht.Y+2*centreCht.Y*coteSecu*coteSecu-sqrt(4*coteSecu*coteSecu*
(3*coteSecu*coteSecu*centreCht.Y*centreCht.Y+centreCht.X*centreCht.X*centreCht.X*centreCht.X+centreCht.X*centreCht.X*centreCht.Y*centreCht.Y+2*centreCht.X*centreCht.X*coteSecu*coteSecu)))/(2*(centreCht.X*centreCht.X+centreCht.Y*centreCht.Y))));
resultat.X=(double) (position.X+((centreCht.X*centreCht.X+centreCht.Y*centreCht.Y-coteSecu*coteSecu-centreCht.Y*resultat.Y)/centreCht.X));
//verfication que le point est dans les limites accessibles
if ((resultat.X>(1050-160*sqrt(2))) || (resultat.X<-1050+160*sqrt(2)) || (resultat.Y>1500-160*sqrt(2)) || (resultat.Y<-1500+160*sqrt(2)))
{
Erreur=true;
resultat.X=position.X;
resultat.Y=position.Y;
}
}
printf ("-> Totem le plus proche: %d\n Coord: X: %f, Y: %f\n",NbTotem,Totem[NbTotem].X,Totem[NbTotem].Y);
}
}
}
//Changement de coordonne pour revenir a la reference initiale: le centre des roues
resultat.X=resultat.X-90*sin(position.Angle);
resultat.Y=resultat.Y-90*cos(position.Angle);
position.X=position.X-90*sin(position.Angle);
position.Y=position.Y-90*cos(position.Angle);
printf ("\nDepart:\nX: %f; Y: %f\nArrive:\nX: %f; Y: %f\nReturn:\nX: %f; Y: %f\n-> Erreur: hors lmite? %d\n",position.X,position.Y,destination.X,destination.Y,resultat.X,resultat.Y,Erreur);
stop;
return EXIT_SUCCESS;
}
b. Programme de grille de détection en C++
#include <cstdlib>
#include <iostream>
#include <math.h>
#include <stdio.h>
#define stop ; system("PAUSE");
using namespace std;
const double cote=(160+40); //on utilise comme obstacle un cercle de rayon "cote" (cote du robot réel+rayon totem)
struct Point
{
double X,Y;
double Angle;
};
struct Traj
{
Point Deb,Fin;
};
int main(int argc, char *argv[])
{
//----------------Declaration des variables----------------
int a,i,j;
double ai,aj,bi,bj,ci,cj,Xint,Yint;
bool TrajBon;
Point Position; //position actuelle
Point Destination; //position a atteindre
Point Totem[5]; //position des 4 totem + un totem fictif (en dehors de la carte habituellement et dedans si on veux eviter le robot adverse)
Point Coin[4]; //position des 4 coins
Point Objet[26]; //position des 4 coins de chaqun des 5 totems,4coins, point de depart et point d'arrive
Traj ListeTraj[325]; //liste des trajectoires possibles
Traj ListeTrajBon[325]; //liste des Bonnes trajectoires possibles
//--------------------------------//
// initialisation des coordonnées //
//--------------------------------//
Position.X=0;
Position.Y=1000;
Destination.X=0;
Destination.Y=1000;
int ConfigTotem=3 ;
Position.Angle=0;
//position des coins
Coin[0].X=-1050;
Coin[0].Y=-1500;
Coin[1].X=1050;
Coin[1].Y=-1500;
Coin[2].X=1050;
Coin[2].Y=1500;
Coin[3].X=-1050;
Coin[3].Y=1500;
//position des centres des totems: on adapte l'initialisation en fonction de la configuration des totems detecté
switch (ConfigTotem)
{
case 1:
Totem[0].X=-680;
Totem[0].Y=-1050;
Totem[1].X=100;
Totem[1].Y=-450;
Totem[2].X=-100;
Totem[2].Y=450;
Totem[3].X=680;
Totem[3].Y=1050;
break;
case 2:
Totem[0].X=-680;
Totem[0].Y=-1050;
Totem[1].X=100;
Totem[1].Y=-450;
Totem[2].X=680;
Totem[2].Y=1050;
Totem[3].X=-680;
Totem[3].Y=1050;
break;
case 3:
Totem[0].X=-680;
Totem[0].Y=-1050;
Totem[1].X=680;
Totem[1].Y=1050;
Totem[2].X=100;
Totem[2].Y=450;
Totem[3].X=-680;
Totem[3].Y=1050;
break;
case 4:
Totem[0].X=100;
Totem[0].Y=-450;
Totem[1].X=-100;
Totem[1].Y=-450;
Totem[2].X=100;
Totem[2].Y=450;
Totem[3].X=-100;
Totem[3].Y=450;
break;
}
Totem[4].X=10000;
Totem[4].Y=10000;
//----------------//
// prog Principal //
//----------------//
//----------------generer la liste de tous les objets----------------
Objet[0].X=Position.X; //pt de depart
Objet[0].Y=Position.Y;
Objet[1].X=Destination.X;
Objet[1].Y=Destination.Y;
a=2;
for (i=0;i<4;i++) //coins
{
Objet[a].X=Coin[i].X;
Objet[a].Y=Coin[i].Y;
a=a+1;
}
for (i=0;i<5;i++) //coins de chaque totem
{
Objet[a].X=Totem[i].X+cote*(sin(Position.Angle)-cos(Position.Angle));
Objet[a].Y=Totem[i].Y+cote*(sin(Position.Angle)+cos(Position.Angle));
a=a+1;
Objet[a].X=Totem[i].X+cote*(sin(Position.Angle)+cos(Position.Angle));
Objet[a].Y=Totem[i].Y+cote*(-sin(Position.Angle)+cos(Position.Angle));
a=a+1;
Objet[a].X=Totem[i].X+cote*(-sin(Position.Angle)+cos(Position.Angle));
Objet[a].Y=Totem[i].Y+cote*(-sin(Position.Angle)-cos(Position.Angle));
a=a+1;
Objet[a].X=Totem[i].X+cote*(-sin(Position.Angle)-cos(Position.Angle));
Objet[a].Y=Totem[i].Y+cote*(sin(Position.Angle)-cos(Position.Angle));
a=a+1;
}
//----------------faire la liste de tous les segments entres chaque objet----------------
a=0;
for (i=0;i<25;i++)
{
for (j=(i+1);j<26;j++)
{
ListeTraj[a].Deb.X=Objet[i].X;
ListeTraj[a].Deb.Y=Objet[i].Y;
ListeTraj[a].Fin.X=Objet[j].X;
ListeTraj[a].Fin.Y=Objet[j].Y;
a=a+1;
}
}
//----------------Transferer dans ListeBon les trajectoires bonnes----------------
a=0;
for (i=0;i<325;i++)
{
TrajBon=true;
for (j=(i+1);j<325;j++) //on verifie si aucun segment j ne coupe le segment i
{
if ((i!=j) && (TrajBon=true))
{
//calcul des coef a,b,c des equations de droite ay+bx=c pour les points i et j
ai=ListeTraj[i].Fin.X-ListeTraj[i].Deb.X;
bi=ListeTraj[i].Deb.Y-ListeTraj[i].Fin.Y;
ci=ListeTraj[i].Deb.Y*ListeTraj[i].Fin.X-ListeTraj[a].Deb.X*ListeTraj[i].Fin.Y;
ai=ListeTraj[j].Fin.X-ListeTraj[j].Deb.X;
bi=ListeTraj[j].Deb.Y-ListeTraj[j].Fin.Y;
ci=ListeTraj[j].Deb.Y*ListeTraj[j].Fin.X-ListeTraj[j].Deb.X*ListeTraj[j].Fin.Y;
if (ai==0)
{
if (aj==0)
{
if (ListeTraj[i].Deb.X==ListeTraj[j].Deb.X)
{
TrajBon=false;
}
}
else
{
//calcul du point d'intersection
Yint=double ((cj-bj*ListeTraj[i].Deb.X)/aj);
//si ce point d'intersection soit a l'interieur des 2 segments
if ((Yint<min(ListeTraj[i].Deb.Y,ListeTraj[i].Fin.Y)) || (Yint>max(ListeTraj[i].Deb.Y,ListeTraj[i].Fin.Y)) || (Yint<min(ListeTraj[j].Deb.Y,ListeTraj[j].Fin.Y))
|| (Yint>max(ListeTraj[j].Deb.Y,ListeTraj[j].Fin.Y)))
{
TrajBon=false;
}
}
}
else
{
//calcul du point d'intersection
Xint=double ((cj-((aj*ci)/ai))/(-((aj*bi)/ai)+bj));
//si ce point d'intersection soit a l'interieur des 2 segments
if ((Xint<min(ListeTraj[i].Deb.X,ListeTraj[i].Fin.X)) || (Xint>max(ListeTraj[i].Deb.X,ListeTraj[i].Fin.X)) || (Xint<min(ListeTraj[j].Deb.X,ListeTraj[j].Fin.X))
|| (Xint>max(ListeTraj[j].Deb.X,ListeTraj[j].Fin.X)))
{
TrajBon=false;
}
}
}
}
if (TrajBon=true)
{
ListeTraj[i].Deb.X=ListeTrajBon[a].Deb.X;
ListeTraj[i].Deb.Y=ListeTrajBon[a].Deb.Y;
ListeTraj[i].Fin.X=ListeTrajBon[a].Fin.X;
ListeTraj[i].Fin.Y=ListeTrajBon[a].Fin.Y;
a=a+1;
}
}
printf ("Nb:%d\n",a);
stop;
return EXIT_SUCCESS;
}
|